As I mentioned in my Artificial Intelligence : OpenAI : Data Use and Privacy post, a key consideration when feeding data and dialogue to a third-party GenAI provider like OpenAI’s ChatGPT relates to data privacy. While investigating what you can do with to toolset, or simply if the data you need is available with an open license an excellent way to start is to use Open Data.
It’s worth noting that just because data is found in a public location does not mean that it is Open Data. Before using the data in this way make sure to check the publishers license. A good source of open data is public government data - for example as published on sites like:
There’s a good list of some sources here: Salesforce tableau : Free Public Data Sets For Analysis
Amazing detail in a few phrases…
Ok - you’ve checked the license and the data is open - it turns out the level of detail that can be generated with Chat-GPT (using GPT-4 and Advanced Data Analytics).
In this example I’m using a medium scale of data with about 1 million rows describing property sales in Connecticut, USA - found on the US government open data site. As per their “Understanding Dataset Pages” guidelines “For the most part, federal agency datasets do not have restrictions on use.” and this dataset has no additional license terms attached.
Having uploaded the CSV file I start with a simple request - and while some parts of the result are less than useful (calculating the mean of a serial number) the overall meaning inference, review of missing data and handful of high level observations is very impressive.
Question 1: “Please summarise and describe this data set.”
And ChatGPT reponds - including Python code used to parse and analyze the data:
Alright, let’s start by loading the data set and taking a look at the first few rows to get a sense of its structure.
import pandas as pd
# Load the dataset
data = pd.read_csv("/mnt/data/Real_Estate_Sales_2001-2020_GL.csv")
# Display the first few rows
data.head()
The dataset appears to pertain to real estate sales from 2001 to 2020. Here’s a breakdown of the columns:
- Serial Number: A unique identifier for each sale.
- List Year: The year in which the sale was listed.
- Date Recorded: The date on which the sale was officially recorded.
- Town: The town where the property is located.
- Address: The address of the property.
- Assessed Value: The value of the property as determined by an assessment.
- Sale Amount: The amount for which the property was sold.
- Sales Ratio: The ratio of the sale amount to the assessed value.
- Property Type: The type of property (e.g., Commercial, Residential).
- Residential Type: If the property is residential, this specifies the type (e.g., Single Family, Condo).
- Non Use Code: A code that might indicate reasons the property is not in use (this seems to have many NaN values).
- Assessor Remarks: Remarks or notes from the assessor (also seems to have many NaN values).
- OPM remarks: Remarks from the OPM (Office of Policy and Management?).
- Location: Location information, possibly coordinates or more detailed info (has many NaN values).
To provide a comprehensive summary, we should:
- Get basic statistics for numerical columns.
- Check the number of missing values for each column.
- Get a sense of the distribution for categorical columns like Town, Property Type, and Residential Type.
Let’s begin with basic statistics for the numerical columns.Finished workingShow work
Here are the basic statistics for the numerical columns:
- Serial Number:
- Range: 0 to 2,000,500,000
- Mean: 431,186
- List Year:
- Range: 2001 to 2020
- Mean: 2010.19
- Assessed Value:
- Range: $0 to $881,510,000
- Mean: $279,143
- 25% of properties have an assessed value of $87,600 or below.
- 50% of properties (median) have an assessed value of $138,390.
- 75% of properties have an assessed value of $225,560 or below.
- Sale Amount:
- Range: $0 to $5,000,000,000
- Mean: $391,151
- 25% of properties were sold for $140,000 or less.
- 50% of properties (median) were sold for $225,000.
- 75% of properties were sold for $365,000 or less.
- Sales Ratio:
- Range: 0 to 1,226,420
- Mean: 10.4464
- 25% of properties have a sales ratio of 0.4867 or below.
- 50% of properties (median) have a sales ratio of 0.6246.
- 75% of properties have a sales ratio of 0.7853 or below.
The sales ratio is supposed to represent the ratio of the sale amount to the assessed value. However, the maximum value of 1,226,420 and a mean of 10.4464 indicate there might be errors or outliers in this column.
Next, let’s check the number of missing values for each column.
# Get distribution for categorical columns
town_distribution = data['Town'].value_counts()
property_type_distribution = data['Property Type'].value_counts()
residential_type_distribution = data['Residential Type'].value_counts()
town_distribution, property_type_distribution, residential_type_distribution
Here’s a summary of the distributions for the categorical columns:
- Town:
- The dataset includes properties from 170 different towns.
- The top three towns by the number of properties are:
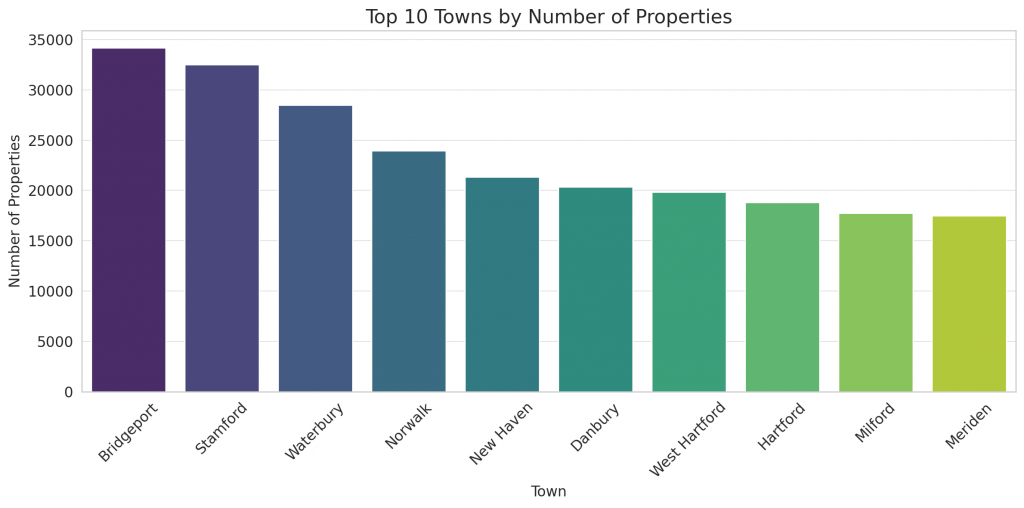
- Bridgeport: 34,201 properties
- Stamford: 32,529 properties
- Waterbury: 28,506 properties
- The town with the least number of properties is labeled “Unknown” with just one property.
- Property Type:
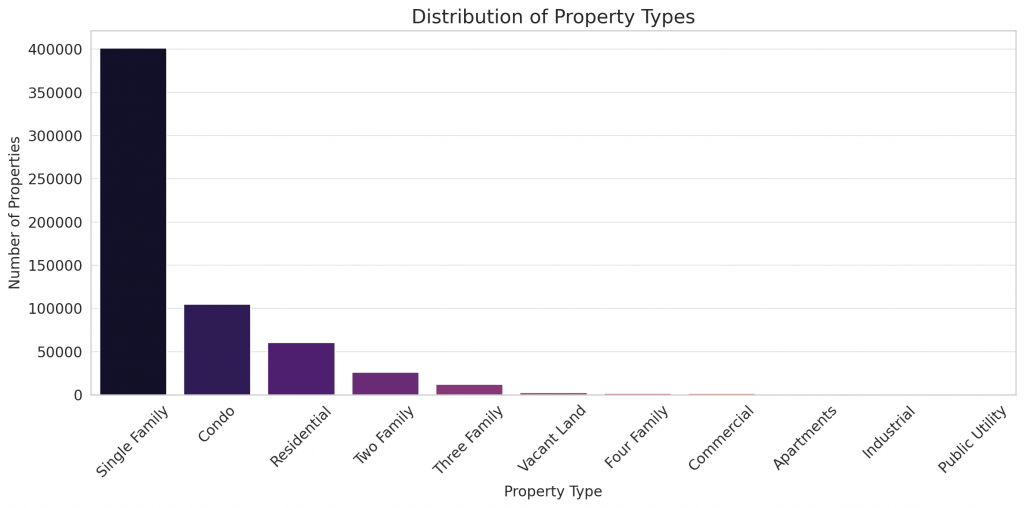
- Single Family: 401,612 properties
- Condo: 105,420 properties
- Residential: 60,728 properties
- Two Family: 26,408 properties
- Three Family: 12,586 propertiesOther property types like Vacant Land, Four Family, Commercial, Apartments, Industrial, and Public Utility have fewer occurrences.
- Residential Type:
- Single Family: 445,016 properties
- Condo: 117,780 properties
- Two Family: 29,609 properties
- Three Family: 14,081 properties
- Four Family: 2,418 properties
To recap, the dataset provides information on real estate sales from 2001 to 2020, with details like address, sale amount, property type, and more. Some columns have a significant number of missing values, and there might be some outliers or errors in the sales ratio column. The dataset covers a wide range of towns and various property types, with single-family residences being the most common.
Would you like any further analysis or specific insights from this dataset?
Question 2: “Visualisations please”
Ok - that was pretty impressive for one sentence, but here’s what I can add for another two words…
Sure! Let’s create visualizations to better understand the data. Here are a few visualizations that might be useful:
- Distribution of Sale Amounts: A histogram to see the distribution of sale prices.
- Distribution of Assessed Values: A histogram to see the distribution of assessed property values.
- Top 10 Towns by Number of Properties: A bar chart to display the towns with the most properties.
- Property Types: A bar chart to see the distribution of different property types.
- Yearly Sales Trends: A line plot to see the number of sales each year.
Let’s start with the distribution of sale amounts.
import matplotlib.pyplot as plt
import seaborn as sns
# Set style
sns.set_style("whitegrid")
# Distribution of Sale Amounts
plt.figure(figsize=(12, 6))
sns.histplot(data < 1e6]['Sale Amount'], bins=50, kde=True, color="skyblue")
plt.title('Distribution of Sale Amounts (under $1,000,000)')
plt.xlabel('Sale Amount')
plt.ylabel('Frequency')
plt.show()
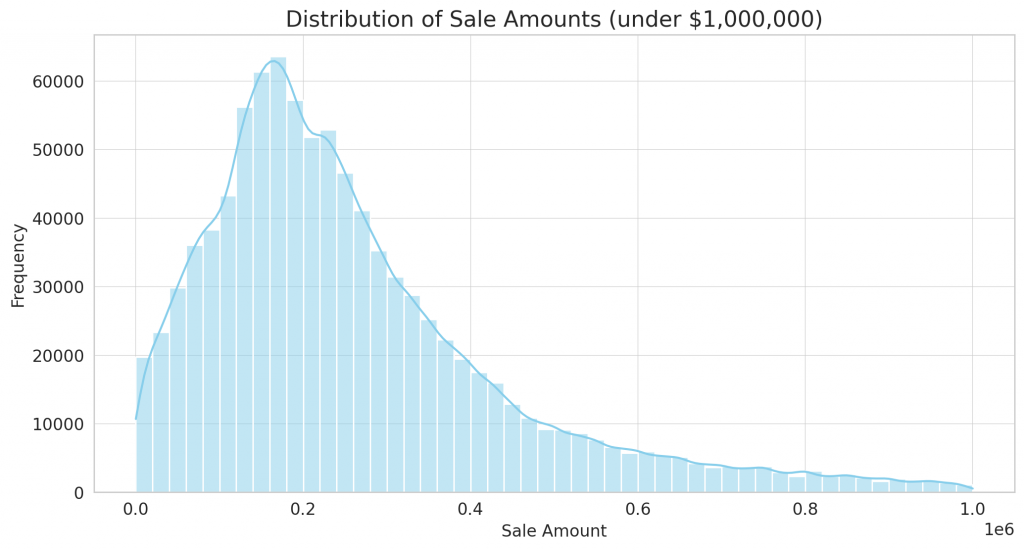
Here’s the distribution of sale amounts for properties sold for under $1,000,000:
- The majority of properties are sold in the range of $100,000 to $300,000.
- The distribution is right-skewed, indicating that a smaller number of properties have higher sale prices within this range.
Next, let’s visualize the distribution of assessed property values.
# Distribution of Assessed Values
plt.figure(figsize=(12, 6))
sns.histplot(data < 1e6]['Assessed Value'], bins=50, kde=True, color="salmon")
plt.title('Distribution of Assessed Values (under $1,000,000)')
plt.xlabel('Assessed Value')
plt.ylabel('Frequency')
plt.show()
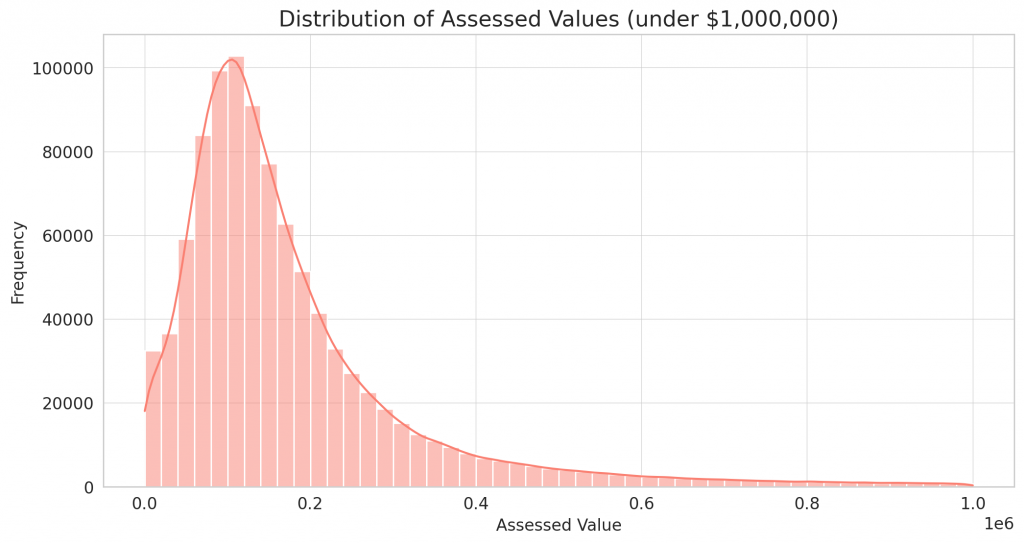
Here’s the distribution of assessed values for properties assessed at under $1,000,000:
- The majority of properties have assessed values in the range of $50,000 to $250,000.
- Similar to the sale amounts, the distribution of assessed values is also right-skewed.
Next, let’s look at the top 10 towns by the number of properties.
# Top 10 Towns by Number of Properties
top_towns = town_distribution.head(10)
plt.figure(figsize=(12, 6))
sns.barplot(x=top_towns.index, y=top_towns.values, palette="viridis")
plt.title('Top 10 Towns by Number of Properties')
plt.xlabel('Town')
plt.ylabel('Number of Properties')
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
The bar chart displays the top 10 towns by the number of properties:
- Bridgeport, Stamford, and Waterbury are the towns with the highest number of properties in the dataset.
Next, let’s visualize the distribution of different property types.
# Distribution of Property Types
plt.figure(figsize=(12, 6))
sns.barplot(x=property_type_distribution.index, y=property_type_distribution.values, palette="magma")
plt.title('Distribution of Property Types')
plt.xlabel('Property Type')
plt.ylabel('Number of Properties')
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
The bar chart showcases the distribution of different property types:
- Single Family properties dominate the dataset, followed by Condo and general Residential types.
- Other property types like Two Family, Three Family, and Vacant Land have significantly fewer occurrences in comparison.
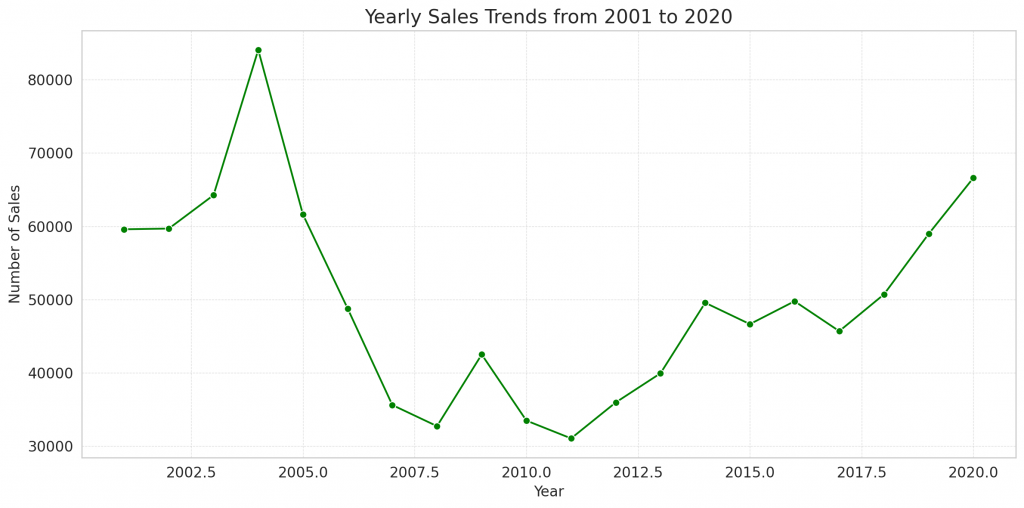
Finally, let’s visualize the yearly sales trends to see the number of sales each year.
# Yearly Sales Trends
yearly_sales = data['List Year'].value_counts().sort_index()
plt.figure(figsize=(12, 6))
sns.lineplot(x=yearly_sales.index, y=yearly_sales.values, marker="o", color="green")
plt.title('Yearly Sales Trends from 2001 to 2020')
plt.xlabel('Year')
plt.ylabel('Number of Sales')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.tight_layout()
plt.show()
The line plot displays the yearly sales trends from 2001 to 2020:
- Sales have seen fluctuations over the years.
- There’s a noticeable dip around 2008-2009, which might be related to the global financial crisis during that time.
- The number of sales started to increase post-2010 and peaked around 2015, after which there has been a slight decline.
These visualizations provide a comprehensive overview of the dataset’s key features. Would you like to explore any other specific aspects or have any further questions?
Question 3: “Could you provide some charts about the properties in Bridgeport, Stamford, and Waterbury?”
This question is about drilling down into the data - and asking ChatGPT to start grouping data together.
Certainly! Let’s focus on the properties in Bridgeport, Stamford, and Waterbury. Here are some visualizations that we can create for these towns:
- Distribution of Sale Amounts: Compare the distribution of sale prices among the three towns.
- Distribution of Assessed Values: Compare the distribution of assessed values among the towns.
- Yearly Sales Trends: See how the number of sales has changed over the years for each town.
- Distribution of Property Types: See the mix of property types in each town.
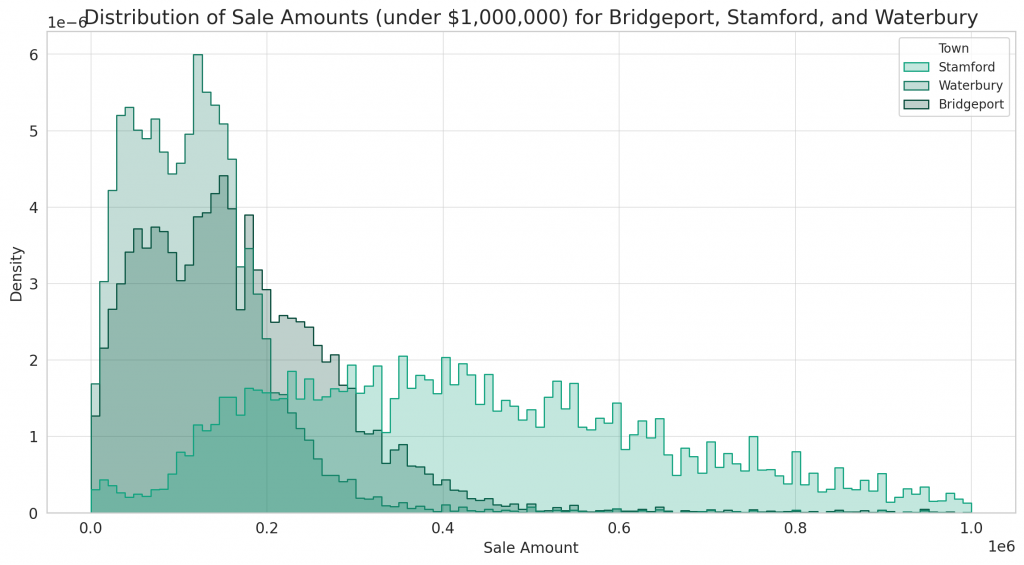
Let’s start with the distribution of sale amounts for Bridgeport, Stamford, and Waterbury.
# Filter data for the three towns
selected_towns_data = data.isin(['Bridgeport', 'Stamford', 'Waterbury'])]
# Distribution of Sale Amounts for the three towns
plt.figure(figsize=(14, 7))
sns.histplot(data=selected_towns_data < 1e6], x='Sale Amount', hue='Town', element="step", stat="density", common_norm=False)
plt.title('Distribution of Sale Amounts (under $1,000,000) for Bridgeport, Stamford, and Waterbury')
plt.xlabel('Sale Amount')
plt.ylabel('Density')
plt.show()
Here’s the distribution of sale amounts for properties sold for under $1,000,000 in Bridgeport, Stamford, and Waterbury:
- Bridgeport and Waterbury have a similar distribution, with the majority of properties sold in the lower price range, approximately between $50,000 and $250,000.
- Stamford has a wider distribution, with a significant number of properties sold in the higher price range, especially between $300,000 and $700,000.
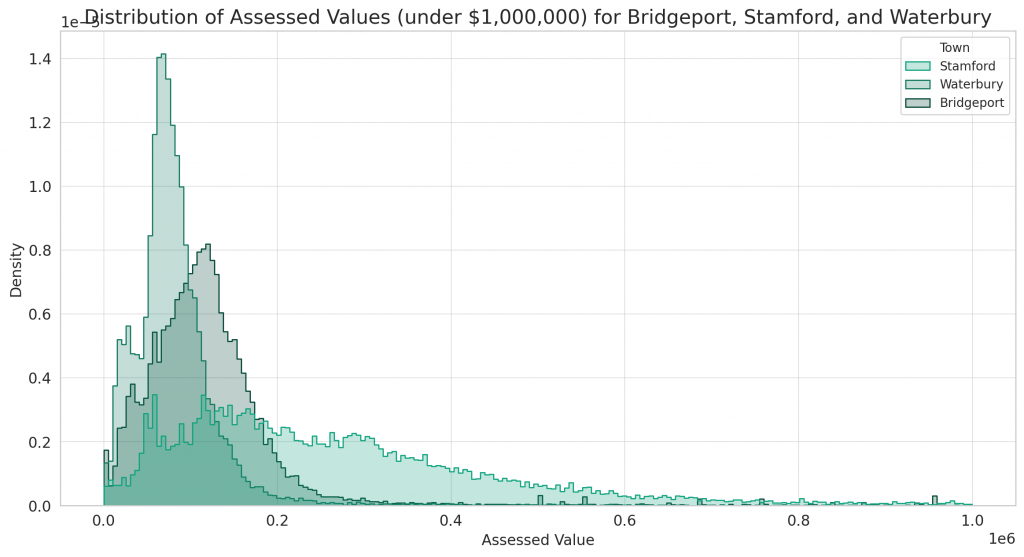
Next, let’s compare the distribution of assessed values among these three towns.
# Distribution of Assessed Values for the three towns
plt.figure(figsize=(14, 7))
sns.histplot(data=selected_towns_data < 1e6], x='Assessed Value', hue='Town', element="step", stat="density", common_norm=False)
plt.title('Distribution of Assessed Values (under $1,000,000) for Bridgeport, Stamford, and Waterbury')
plt.xlabel('Assessed Value')
plt.ylabel('Density')
plt.show()
The chart displays the distribution of assessed values for properties valued under $1,000,000 in Bridgeport, Stamford, and Waterbury:
- Bridgeport and Waterbury again exhibit a similar distribution, with a concentration of properties having assessed values in the lower range.
- Stamford stands out with a broader distribution, indicating a mix of property values, with a significant portion having higher assessed values.
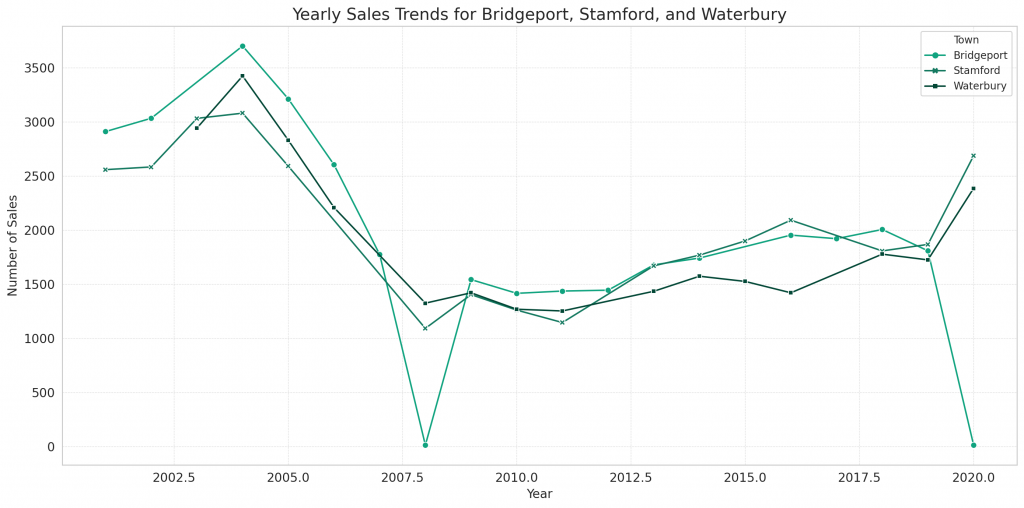
Next, let’s explore the yearly sales trends for these three towns.
# Yearly Sales Trends for the three towns
yearly_sales_selected_towns = selected_towns_data.groupby(['List Year', 'Town']).size().unstack()
plt.figure(figsize=(14, 7))
sns.lineplot(data=yearly_sales_selected_towns, markers=True, dashes=False)
plt.title('Yearly Sales Trends for Bridgeport, Stamford, and Waterbury')
plt.xlabel('Year')
plt.ylabel('Number of Sales')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.tight_layout()
plt.show()
The line plot displays the yearly sales trends for Bridgeport, Stamford, and Waterbury from 2001 to 2020:
- Bridgeport has consistently had the highest number of sales among the three towns. There was a significant drop in sales around 2008-2009, but sales have since rebounded and remained relatively steady.
- Stamford follows a similar trend to Bridgeport but has a slightly lower volume of sales.
- Waterbury saw a decline in sales around the 2008-2009 period, similar to the other towns, and has fluctuated in subsequent years.
Lastly, let’s examine the distribution of property types in each of the three towns.
# Distribution of Property Types for the three towns
property_type_selected_towns = selected_towns_data.groupby(['Town', 'Property Type']).size().unstack()
# Plotting
property_type_selected_towns.plot(kind='bar', stacked=True, figsize=(14, 7))
plt.title('Distribution of Property Types for Bridgeport, Stamford, and Waterbury')
plt.xlabel('Town')
plt.ylabel('Number of Properties')
plt.xticks(rotation=0)
plt.tight_layout()
plt.show()
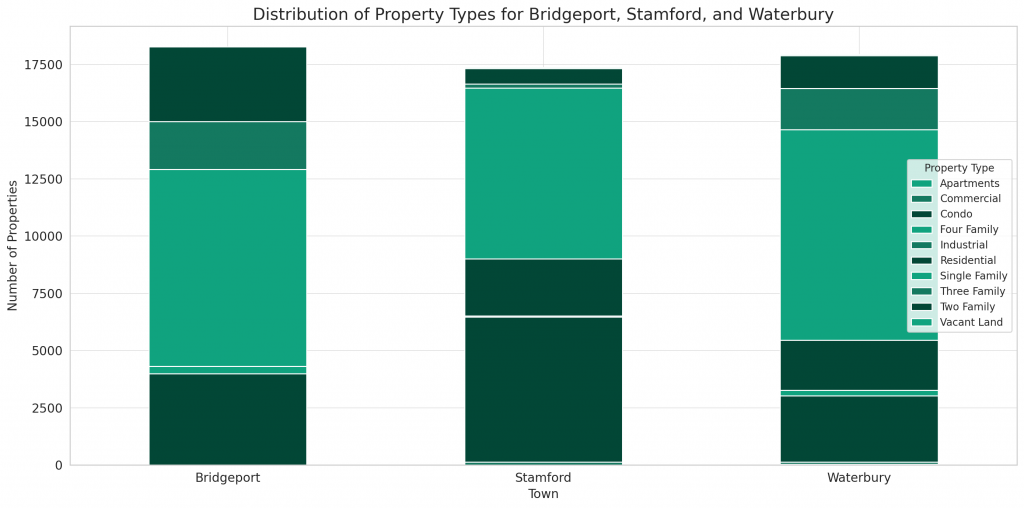
The stacked bar chart illustrates the distribution of property types for Bridgeport, Stamford, and Waterbury:
- For all three towns, Single Family properties are predominant.
- Condos make up a significant portion, especially in Stamford.
- The other property types, like Two Family, Three Family, and Vacant Land, have fewer occurrences, but they still constitute a noticeable proportion in Bridgeport and Waterbury.
These visualizations provide insights into the property market dynamics of Bridgeport, Stamford, and Waterbury, highlighting differences and similarities among them.
Would you like any further analysis or have additional questions about these towns or the dataset?
Question 4: “Can you find (and chart) any correlation between OPM remarks and sale amounts?”
This is one of those questions which could lead so easily to an AI hallucination (eg. a confident statement seemingly in contradiction to fact / training data fed into the model). After all humans are seeing correlations and assuming causation all the time.
But one of the nice features of the OpenAI Advanced Data Analytics is the live code being generated before each output - this allows us to review the code (and even review and run it ourselves) to validate the outputs.
For the question above the response was:
Certainly! To assess any correlation between the “OPM remarks” and “Sale amounts,” we’ll first need to understand the unique values and the distribution of “OPM remarks.”
Let’s start by examining the unique values in the “OPM remarks” column.
# Unique values and their counts in the "OPM remarks" column
opm_remarks_distribution = data['OPM remarks'].value_counts()
opm_remarks_distribution
The “OPM remarks” column has a wide variety of unique remarks, with 4,825 different remarks to be precise. The most frequent remarks include:
- “GOOD SALE PER MLS” (978 occurrences)
- “NO MLS” (500 occurrences)
- “NEW CONSTRUCTION” (345 occurrences)
- “SHORT SALE PER MLS” (326 occurrences)
- “TOTAL RENOVATION PER MLS” (316 occurrences)
Given the vast number of unique remarks, it might be more meaningful to focus on the most frequent remarks when assessing any correlation with sale amounts. This approach will help ensure we have a sufficient sample size for each remark to draw meaningful conclusions.
Let’s visualize the sale amounts for properties associated with the top 5 most frequent OPM remarks.
# Filter data for the top 5 OPM remarks
top_opm_remarks_data = data.isin(opm_remarks_distribution.head(5).index)]
# Box plot for Sale Amounts associated with top 5 OPM remarks
plt.figure(figsize=(14, 8))
sns.boxplot(data=top_opm_remarks_data, x='OPM remarks', y='Sale Amount', showfliers=False, palette="coolwarm")
plt.title('Distribution of Sale Amounts for Top 5 OPM Remarks')
plt.xlabel('OPM Remarks')
plt.ylabel('Sale Amount')
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
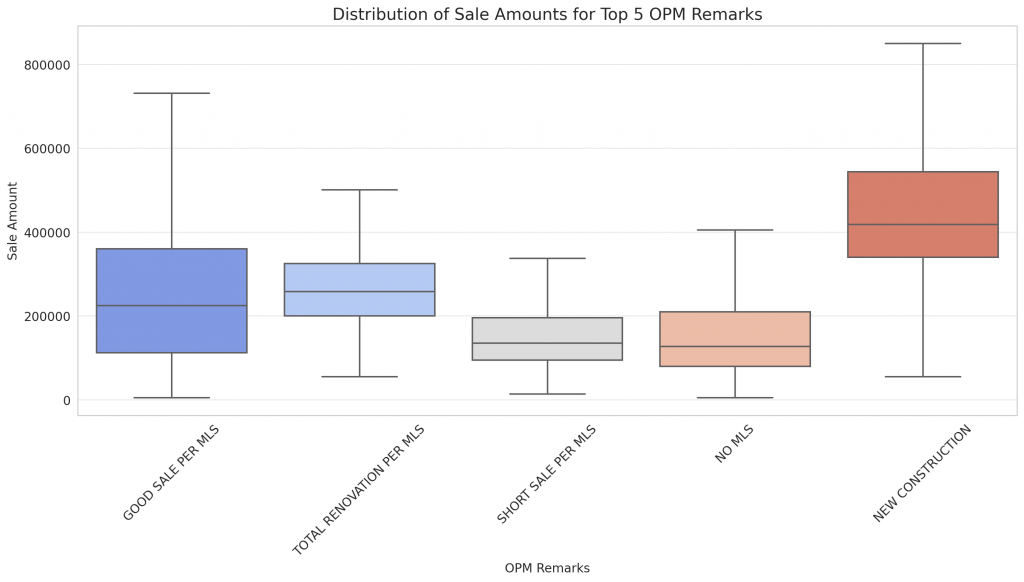
The box plot provides a visual representation of the distribution of sale amounts for properties associated with the top 5 most frequent OPM remarks:
- The median sale amount varies across the different remarks. For instance, properties with the remark “NEW CONSTRUCTION” tend to have a higher median sale price compared to those with “SHORT SALE PER MLS”.
- The interquartile range (IQR), represented by the height of the boxes, also varies across remarks. This indicates the spread or variability in sale amounts within each category.
From the plot, we can observe distinct differences in sale amounts across the different OPM remarks. However, to quantify the strength and direction of the linear relationship between the two categorical variables, we can use a statistical measure like Cram?r’s V.
In summary…
The level of detail available with minimal prompting is impressive and verifiable by reviewing the code.
Observations need to be considered a little more carefully for cases like hallucinations, but as you have the data, the code and the charts to hand that’s a little easier than when asking for long hand prose about a topic.